//! # 题目描述
//!
//! 给定一个长度为 `n` 的整数数组 `height` 。有 `n` 条垂线，第 `i` 条线的两个端点是 `(i, 0)` 和 `(i, height[i])` 。
//! 
//! 找出其中的两条线，使得它们与 `x` 轴共同构成的容器可以容纳最多的水。
//! 
//! 返回容器可以储存的最大水量。
//! 
//! 说明：你不能倾斜容器。
//! 
//!  
//! 
//! 示例 1：
//!
//! ![Image](/images/question_11.jpg)
//!
//! ```plain
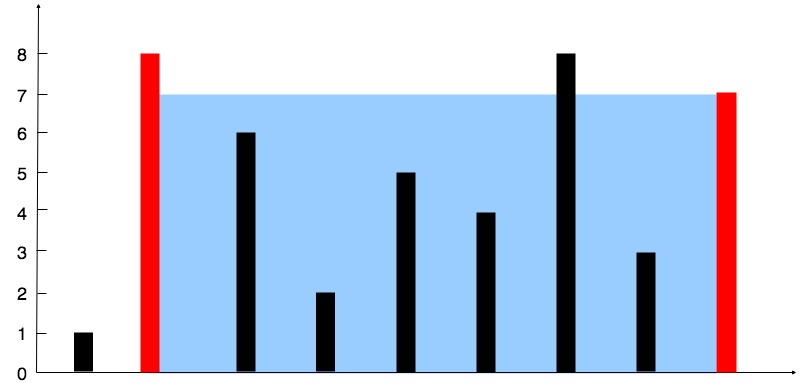
//! 输入：[1,8,6,2,5,4,8,3,7]
//! 输出：49 
//! 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。
//! ```
//!
//! 示例 2：
//! 
//! ```plain
//! 输入：height = [1,1]
//! 输出：1
//! ```
//! 
//! 提示：
//!
//! - `n == height.length`
//! - `2 $\leqslant$ n $\leqslant$ $10^5$`
//! - `0 $\leqslant$ height[i] $\leqslant$ $10^4$`
//! 
//! 您可以在 <https://dongs.xyz/post/algorithm-container-with-most-water/> 查看关于此问题的分析博文。
//!
//! Sources: <https://leetcode.cn/problems/container-with-most-water/>

////////////////////////////////////////////////////////////////////////////////

/// 盛最多水的容器
///
/// # 参数
/// * `height` - 由器壁高度组成的数组
pub fn max_area(height: Vec<i32>) -> i32 {
    alg_1(height)
}

use core::cmp::max;

/// 遍历整个数组，找到最大容水量的器壁组合
/// 
/// # 参数
/// * `height` - 由器壁高度组成的数组
fn alg_1(height: Vec<i32>) -> i32 {
    let mut sidx: usize = 0;
    let mut eidx = height.len() - 1;
    let mut area_max = 0;
    let area = |x: usize, y: usize| -> i32 {
        return if height[x] >= height[y] {
            height[y]
        } else {
            height[x]
        } * (if x >= y { x - y } else { y - x }) as i32;
    };

    loop {
        if sidx == eidx {
            break;
        }
        area_max = max(area(sidx, eidx), area_max);
        let mut moved = false;
        if height[sidx] <= height[eidx] {
            while sidx < eidx {
                if height[sidx + 1] <= height[sidx] {
                    sidx += 1;
                    moved = true;
                } else {
                    break;
                }
            }
            if !moved {
                sidx += 1;
            }
        } else {
            while sidx < eidx {
                if height[eidx - 1] <= height[eidx] {
                    eidx -= 1;
                    moved = true;
                } else {
                    break;
                }
            }
            if !moved {
                eidx -= 1;
            }
        }
    }

    area_max
}